DIARIO 2 TERCER PARCIAL

 FARCCIONES PARCIALES

Las fracciones parciales son una técnica de descomposición de fracciones algebraicas, que se utilizan principalmente para simplificar o integrar funciones racionales más complejas. Esta técnica se aplica a funciones que están en forma de una fracción de dos polinomios, donde el grado del numerador es menor o igual al grado del denominador.

El proceso de fracciones parciales consiste en descomponer una función racional en una suma de fracciones más simples. Estas fracciones más simples se expresan como una suma de términos, cada uno de los cuales tiene un denominador irreducible (es decir, no se puede factorizar más). A continuación, se muestra el procedimiento general para encontrar las fracciones parciales de una función racional:

Así:

2x−2 + 3x+1 = 2(x+1) + 3(x−2)(x−2)(x + 1)

Lo cual puede simplificarse usando Expresiones Racionales. Queda así:

= 2x+2 + 3x−6x²+x−2x−2

= 5x−4x²−x−2

El método se llama "Descomposición en fracciones parciales" y es así:

Paso 1: Factoriza lo de abajo

Paso 2: Escribe una fracción parcial para cada uno de esos factores

Paso 3: Multiplica todo por lo de abajo para que ya no tengamos fracciones

Paso 4: Ahora encuentra las constantes A₁ y A₂

Sustituir las raíces (los "ceros") de (x−2)(x+1) puede ayudar:

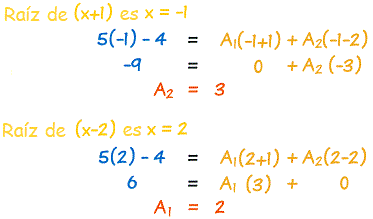
Y tenemos nuestra respuesta:

https://www.disfrutalasmatematicas.com/algebra/fracciones-parciales.html