Longitud del arco de la curva y = f (x)

fórmula general

En aplicaciones anteriores de integración, requeríamos que la función f (x) fuera integrable, o al menos continua. Sin embargo, para calcular la longitud de arco tenemos un requisito más estricto para f(x). Ahora, requerimos que f(x) sea diferenciable, y además que su derivada, f ‘(x), sea continua. Las funciones como esta, que tienen derivadas continuas, se denominan suaves. (Esta propiedad vuelve a aparecer en capítulos posteriores).

Sea f(x) una función suave definida sobre [a, b]. Queremos calcular la longitud de la curva desde el punto (a, f (a)) hasta el punto (b, f (b)). Comenzamos usando segmentos de recta para aproximar la longitud de la curva. Para i = 0, 1, 2, …, n, sea P = {xi} una partición regular de [a, b]. Luego, para i = 1, 2, …, n, se construye un segmento de recta desde el punto (xi − 1, f(xi − 1)) hasta el punto (xi, f(xi)). Aunque parezca lógico usar segmentos de recta horizontales o verticales, queremos que nuestros segmentos de recta se aproximen a la curva lo más posible. La figura 6.14 muestra esta construcción para n = 5.

Figura 6.14 Podemos aproximar la longitud de una curva agregando segmentos de recta.

Para auxiliarnos en el cálculo de la longitud de cada segmento de recta, observamos el cambio en la distancia vertical, así como el cambio en la distancia horizontal en cada intervalo. Como hemos usado una partición regular, el cambio en la distancia horizontal en cada intervalo viene dado por Δx. Sin embargo, el cambio en la distancia vertical varía de un intervalo a otro, por lo que usamos Δyi = f(xi) − f(xi − 1) para representar el cambio en la distancia vertical durante el intervalo [xi − 1, xi], como se muestra en Figura 6.15. Tenga en cuenta que algunos (o todos) los Δyi pueden ser negativos.

Figura 6.15 Un segmento de recta representativo aproxima la curva sobre el intervalo cerrado [xi − 1, xi].

Según el teorema de Pitágoras, la longitud del segmento de recta es

También podemos escribir esto como

Ahora, según el teorema del valor medio, hay un punto xi* ∈ [xi − 1, xi] tal que f ′ (xi*) = (Δyi) / (Δx). Entonces la longitud del segmento de recta viene dada por

Sumando las longitudes de todos los segmentos de recta, obtenemos la siguiente aproximación para la longitud del arco

Esta es una suma de Riemann. Tomando el límite cuando n → ∞, obtenemos

Resumimos estos hallazgos en el siguiente teorema.

Teorema 6.4.1. Longitud del arco para y = f (x)

Sea f (x) una función suave en el intervalo cerrado [a, b]. Entonces, la longitud del arco de la porción de la gráfica de f (x) desde el punto (a, f (a)) hasta el punto (b, f (b)) viene dada por

Tenga en cuenta que estamos integrando una expresión que involucra f ′(x), por lo que debemos asegurarnos de que f ′(x) sea integrable. Es por eso que requerimos que f (x) sea suave.

Ejemplo ilustrativo 6.4_1 Cálculo de la longitud de arco de una función de x

Sea f (x)=2x3/2. Calcula la longitud del arco de la gráfica de f (x) sobre el intervalo [0, 1]. Redondea la respuesta a tres decimales.

Solución:

Tenemos f ′(x) = 3x1/2, entonces [f ′(x)]2 = 9x. Entonces, la longitud del arco es

Esta imagen tiene un atributo ALT vacío; su nombre de archivo es image-1.png

Se sustituye u = 1 + 9x, entonces, du = 9dx. Cuando x = 0, entonces u = 1, y cuando x = 1, entonces u =10. Por lo tanto,

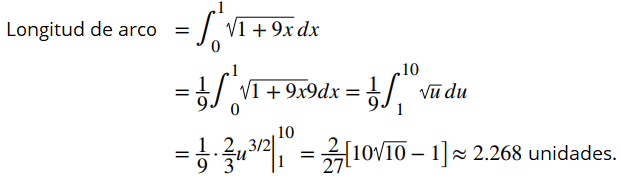
Esta imagen tiene un atributo ALT vacío; su nombre de archivo es image-2.png

♦

Aunque es bueno tener una fórmula para calcular la longitud del arco, este teorema particular puede generar expresiones que son difíciles de integrar. Estudiamos algunas técnicas para la integración en Introducción a las técnicas de integración. En algunos casos, es posible que tengamos que usar una computadora o una calculadora para aproximar el valor de la integral.

Longitud del arco de la curva x = g(y)

Acabamos de ver cómo aproximar la longitud de una curva con segmentos de recta. Si queremos encontrar la longitud del arco de la gráfica de una función de y, podemos repetir el mismo proceso, excepto que dividimos el eje y en lugar del eje x. La figura 6.16 muestra un segmento de recta representativo.

Figura 6.16 Un segmento de recta representativo en el intervalo [yi − 1, yi].

Tenemos que la longitud del segmento de recta es

que también se puede escribir como

Si ahora seguimos el mismo desarrollo que hicimos anteriormente, obtenemos una fórmula para la longitud del arco de una función x = g(y).

Teorema 6.4.2. Longitud del arco para x = g(y)

Sea g(y) una función suave en un intervalo cerrado [c, d]. Entonces, la longitud del arco de la gráfica de g(y) desde el punto (c, g(c)) hasta el punto (d, g(d)) viene dada por